Davide Michieletto
Current PhD Student under supervision of Prof. M. Turner (Warwick), Dr. G. Alexander (Warwick) and Dr. D. Marenduzzo (Edinburgh) and collaborating with Prof. Enzo Orlandini (Padova). My main interest is in studying the physics behind systems of bio-polymers like DNA. I also enjoy making soap films collapse:
Publications (for a full version look also here)
- Y Timofeeva, S Coombes, D Michieletto, Gap junctions, dendrites and resonances: a recipe for tuning network dynamics
 , The Journal of Mathematical Neuroscience, 2013, 3 (1), 15
, The Journal of Mathematical Neuroscience, 2013, 3 (1), 15
- D. Michieletto, D. Marenduzzo, E. Orlandini, G. P. Alexander, M. S. Turner, Threading Dynamics of Ring Polymers in a Gel
 , ACS Macro Lett., 2014, 3, pp 255-259 (arXiv:1306.4965
, ACS Macro Lett., 2014, 3, pp 255-259 (arXiv:1306.4965 )
) - D. Michieletto, D. Marenduzzo, E. Orlandini, G. P. Alexander, M. S. Turner, Dynamics of Self-Threading Ring Polymers in a Gel
 , Soft Matter, 2014, 10, pp 5936-5944 (arXiv:1403.5418
, Soft Matter, 2014, 10, pp 5936-5944 (arXiv:1403.5418 )
)
- D. Michieletto, D. Marenduzzo, E. Orlandini, Is the Kinetoplast DNA a Percolating Network of Linked Rings at its Critical Point?, Phys. Biol., 2015, 12, 036001 (arXiv:1406.0141
 )
)
- D. Michieletto, D. Marenduzzo, M. S. Turner, Topology Regulation during Replication of the Kinetoplast DNA, arXiv:1408.4237 (Submitted to Phys. Biology)
- D. Michieletto, M. Baiesi, E. Orlandini and M. S. Turner, Rings in Random Environments: Sensing Disorder Through Topology, Soft Matter, 2015, 11, pp 1100-1106 (arXiv:1410.5980)
- D. Michieletto, D. Marenduzzo, E. Orlandini, Topological Patterns in two-dimensional gel electrophoresis of DNA knots, PNAS (to appear), (arXiv)
MSc Complexity: MiniProject1: Exploring Gap Junctions locations and density in a network of model neurons with resonant dendrites (Dr Yulia Timofeeva) (From March to June 2012)
The Report can be found at: Report 1st Mini-Project
MSc Complexity: MiniProject2: Topological Glasses (Prof. Matthew Turner) (From June to Sept. 2012)
The Report can be found at: Report Topological Glasses
Ring Polymers in Gel:
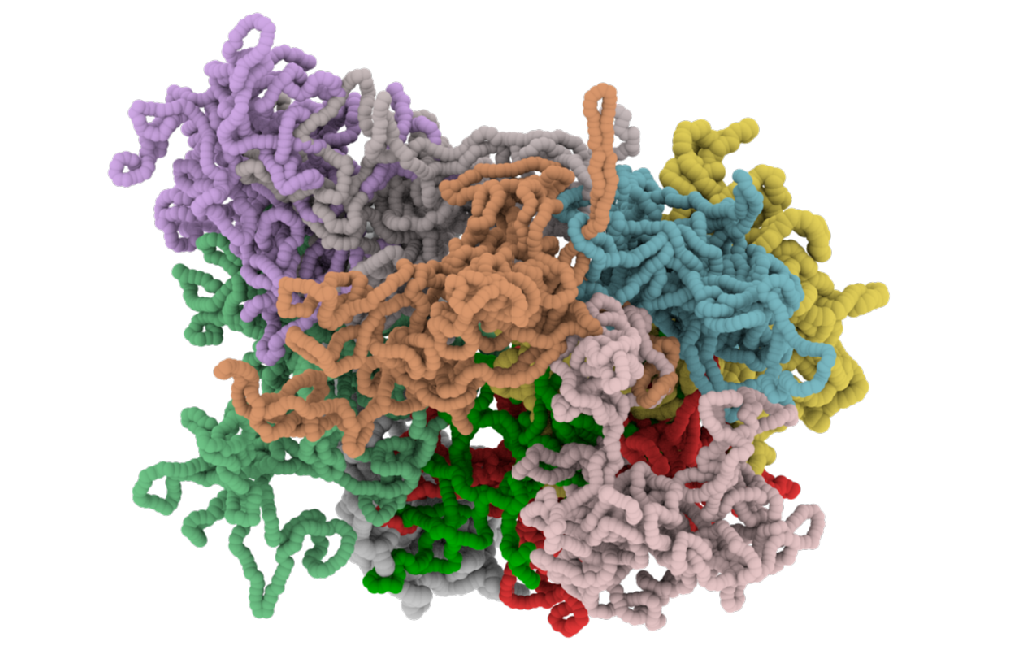
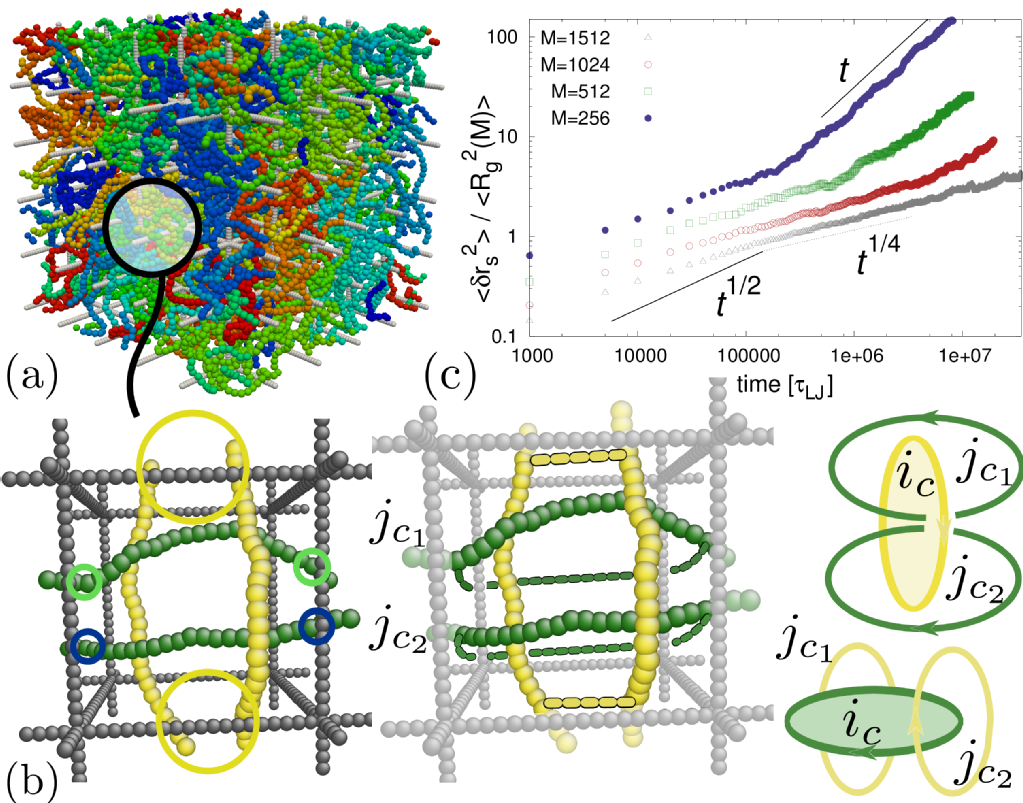
Ring polmyers (such as DNA plasmids) possess many properties which are intimately related to their topological state. Because of their closed shape, they have a well defined topology, i.e. linked, knotted, etc. , which has to be preserved during dynamics. This allows for special features which characterise systems made of ring polymers, such as artificial melt of rings or a dense packing of chromatin inside cell's nucleus. The study of dense solutions of ring polymers can help to develop materials with unique viscoelastic properties or shed a deeper understanding on the dyanmics and organisation of higher-order DNA strucutres. We studied in depth the constraint that rings are subjected to when protruding through each other (also called threadings). We showed that these threadings can slow down of the rings dynamics. Ultimately, these constraints can form a hierarchical structures which leads to a frozen, i.e. glassy, state of the system.
(click on image for link to the paper)
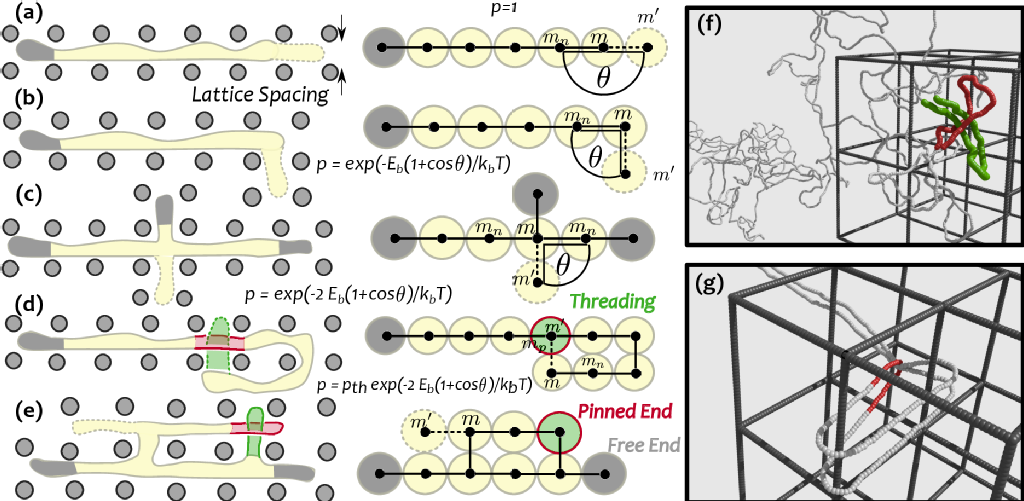
Another effect related to threading is when a very long ring polymer threads through itself. In this case, also in very dilute conditions, a ring can severely slow down its own diffusion. We developed an algorithm to take into account this type of long-ranged correlations on the dynamics of isolated rings in gel. When an electric field is applied, rings can self-trap around gel obstacles as in the figure below. Self-trapping of rings polymers during gel electrophoresis experiments has not received a satisfactory explanation yet. This can shed some light on the dyanmics of how self-trapping takes place and how this can be distinguished from other types of slowing down.
(click on image for link to the paper)
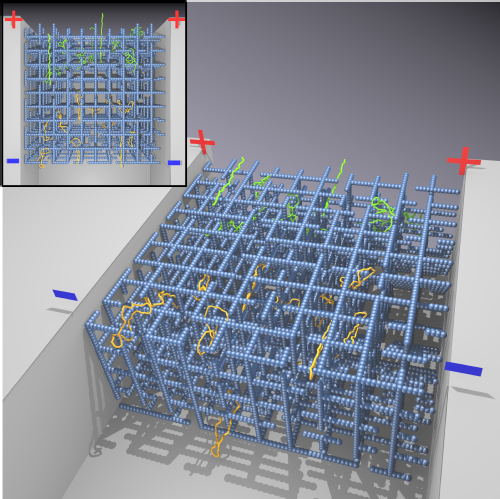
We recently also developed a coarse-grained mofdel to study the dynamics of polymers with different topologies driftin through a physical gel, i.e. a gel that presents dangling ends. These are modelled as broken bonds in a 3D cubic lattice, and provide a cosntraint on the dynamics of the polymers when they have closed topology. Because rings get hung up, they tend to drift much more slowly than their linear cousins, although high external fields need to be used to observe this phenomenon.
Collective Motion in Confining and Non-Differentiable Geometries (January 2011): MScThesis
The thesis focused on the numerical and analytical study of self-organising properites of self-propelled round particles enbedded in 2D confining and strongly irregular geometries.We observed already well known properties as phase transition from disordered state to ordered one, described by Vicsek scalar order parameter. We studied the effects on the phase transition due to (i) hard-core interaction among the particles, (ii) finite size system, (iii) different types of boundary conditions and (iv) irregular boundaries.
We then studied how these features affect the clustering properties and the spatial correlation. Moreover, we observed a dependence of the giant density fluctuations on the size of the system. As far as we know, this is the first time this phenomenon has been studied. We then used constraints on the boundary such that the particles were forced to slip along the walls once they interact with each-other. These boundary conditions allowed us to reproduce qualitatively and quantitatively experiments performed with real self-propelled particles and rods (as bacteria). In appendix we indeed show that the numerical results obtained after the introduction of a funnel in the system are according with the experiment performed by Austin et. al. (P. Galajda, J. Keymer, P. Chaikin, R. Austin "A Wall of Funnels Concentrates Swimming Bacteria" Journal of Bacteriology 189, 23 (200)).

e-mail contact:
d.michieletto@warwick.ac.uk
If you feel very nerd, or you want to test it:
Videos of Collective Motion in Confined Geometries: