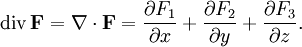Seminar1
OBJECTIVES
At the end of this seminar, the reader should be able to able to derive Basic Governing Equations for Compressible/Incompressible equations which include continuity equation, Momentum equation and Energy equation.
BASIC CONCEPTS
- A System is defined as an arbitrary quantity of mass of fixed identity. Everything external to system is called its surrounding and the system is separated from its surroundings by boundaries.
- A control volume is a mathematical abstraction employed in the process of creating mathematical models of physical processes. In an inertial frame of reference, it is a fixed volume in space through which the fluid flows. The surface enclosing the control volume is referred to as control surface.
- In continuum assumption, Fluid is considered as continuous such that fluid properties are continuous functions of spatial coordinates.
- MASS CONSERVATION: Mass of a system is conserved i.e it can neither be created nor destroyed.
- The rate of change of momentum equals the sum of the forces on a fluid particle. (Newton 's second law of motion)
- First Law of Thermodynamics:The increase in the internal energy of a system is equal to the amount of energy added by heating the system, minus the amount lost as a result of the work done by the system on its surroundings.

- Divergence of a Vector:Let x, y, z be a system of Cartesian coordinates on a 3-dimensional space, and let i, j, k be the corresponding unit vectors.
The divergence of a continuously differentiable vector field F = F1 i + F2 j + F3 k is defined as
- Substantive (Total) Derivative:

Where
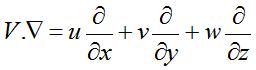
-
Reynold Transport theorem: The Reynolds transport theorem refers to any extensive property, N, of the fluid in a particular control volume. It is expressed in terms of a substantive derivative on the left-hand side.
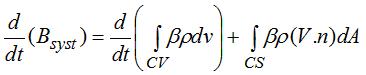
STUDY MATERIAL
For study material, See Reference1
Back ground Study material
For better understanding of the derivations, It is recommended that before reading this material following topics must be read in detail
- Pressure force and equilibrium of a fluid (Reference 2)
- Reynold transport theorem (Reference 3)
- Conservation of Mass (Reference 4)
- The Linear Momentum Equation (Reference 5)
- The energy equation (Reference 6)
The Derivation of Differential equation for Energy is better explained in Reference 7.
Detailed FInite Volume Formulation of Naiver-stokes equations can be found in Reference 8.
REFERENCES
- Fluid Mechanics by FRANK M WHITE page 225-249
- Fluid Mechanics by FRANK M WHITE page 65
- Fluid Mechanics by FRANK M WHITE page 139
- Fluid Mechanics by FRANK M WHITE page 147
- Fluid Mechanics by FRANK M WHITE page 153
- Fluid Mechanics by FRANK M WHITE page 172
- Viscous Flow by FRANK M White page 69
- An introduction to Computational Fluid Dynamic; The Finite Volume Approach by HK Vesteeg & W Malalasekera Chapter2