Epidemic control
Mathematical models can play a key role in preparing for epidemics and pandemics. It particular, (i) models can be used to generate a range of feasible senarios such that the necessary logistical capacity can be assessed; (ii) models can be used to test a wide variety of control strategies and hence determine optimal responses for a given set of resources and constraints; (iii) finally, the use of a mathematical modelling framework is an ideal mechanism for focusing of those aspects of transmission where parameters or detail epidemiological knowledge is required.
For human pathogens, work in this area includes control measures against smallpox, pandemic influenza and SARS -- more details below. Much of the methodology and many of the results associated with network models are applicable for understanding the control of epidemics.
For animal pathogens, work on epidemic predict and control includes foot-and-mouth disease , bovine TB and H5N1 in poultry .
Implications of Household Structure for Pandemic Control
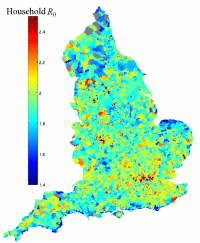 One important public-health question is to determine what role households play in epidemics. We have taken a model where households exist as tightly clustered cliques , with transmission between housholds being random; in addition it is assumed that the transmission rate between individuals within a household (τ) is significantly greater than the transmission rate between individuals in different households (β). The values of τ and β are then set such that the basic reproductive ratio (R0) of the infection is 2, which is a reasonable approximation for pandemic influenza.
One important public-health question is to determine what role households play in epidemics. We have taken a model where households exist as tightly clustered cliques , with transmission between housholds being random; in addition it is assumed that the transmission rate between individuals within a household (τ) is significantly greater than the transmission rate between individuals in different households (β). The values of τ and β are then set such that the basic reproductive ratio (R0) of the infection is 2, which is a reasonable approximation for pandemic influenza.
The graph on the right shows how R0 varies across ward-level areas of England for parameters that overplay the importance of within-household transmission. The result that varying household structure throughout the country affects R0 for a disease is, however, robust.
Research is also investigating where targetting various control methods towards households rather than individuals is an effective strategy.
Using the 2001 Census Movement Data to Predict the Spread of Infections.
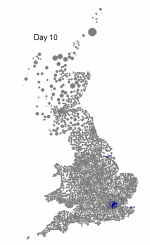
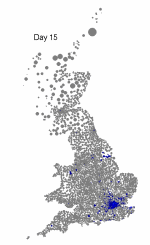
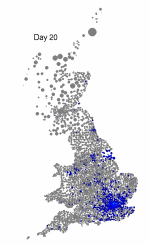
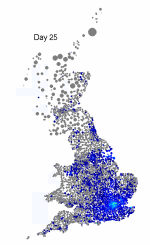
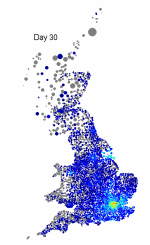
The above maps show the spread of a short-generation pathogen from a small number of initial cases in London. Spread throughout most of the UK has occurred within 30 days highlighting the need for rapid implementation of controls. Results are obtained by simulating the "meta-population" dynamics of infection within 10,000 wards in the UK; the spatial spread of infection is achieved using the work-place locations recorded in the 2001 census.
Simulation Models of Pathogen Spread and Control on Networks
The threat of covert release of infectious pathogens by terrorists and the emergence of novel zoonotic and human diseases presents healthcare authorities with difficult tests of management policies, and the appropriate and proportionate response to the allocation of resources. From a disease control perspective it is of fundamental importance to identify when an epidemic may be best controlled using targeted response (e.g. contact tracing and quarantining of individuals) compared to a blanket response (such as mass vaccination, or culling in the case of livestock diseases).
Using an explicit network of contacts (assumed to be representative of the UK population), Jon Read and Matt Keeling have developed a model of covert smallpox release and infection within a small population. We have applied various control options (quarantine, contact tracing and mass vaccination) to identify the ideal control strategy for a given situation. Network structure has a profound influence on the appropriate response to such outbreaks.
Publications
HJ Wearing, P Rohani, MJ Keeling (2005). Appropriate models for the management of infectious diseases . PLoS Medicine 2, 621-627.
NM Ferguson, MJ Keeling, WJ Edmunds, R Gani, BT Grenfell, RM Anderson, S Leach (2003). Planning for smallpox outbreaks. Nature 425, 681-685.
