Daniel Turner
Undergraduate degree - BSc Mathematics
After leaving secondary school in 2005, with A-levels in Mathematics, Further Mathematics, Physics, Chemistry, and ICT, I started studying Mathematics at the University of Warwick. During the three years of study that followed, I found that I had greater interest in modules about applied mathematics such as Mathematical Biology and Fluid Dynamics. I graduated in the summer of 2008 with a BSc Hons (2.1) in Mathematics.
MOAC MSc in Mathematical Biology and Biophysical Chemistry
After my maths degree, I found that none of the traditional "mathematician's careers", such as banking and finance, really appealed to me, and neither did the prospect of further study in pure mathematics. I decided that I wanted to find a way to apply my interest and skills in mathematics to other problems in "the real world". My search for such a programme brought me to MOAC Doctoral Training Centre.
During the taught section of the MSc, I picked up a lot of new knowledge in the areas of cellular biology, biochemistry, and statistics. I also gained vital experience of how to work efficiently and safely in a laboratory environment.
For the research section of the course, I worked on the following miniprojects:
- Time-resolved biosensor development: Culture and purification of fusion antibody (Prof. Richard Napier, Warwick HRI)
During this project, I learned how to use bacterial cell cultures (in this project, E. coli colonies) to express a protein, then how to extract this protein from the culture and purify the protein using Fast Performance Liquid Chromatography (FPLC). I also used isothermal calorimetry as a means of testing for the activity of the purified protein sample.
- Stochastic eradication-resolution dynamics (Dr. Hugo van den Berg, Mathematics)
This project was concerned with modelling the eradication of some sort of infection/disease from an organism by its immune response. Using a model which combined a deterministic description of the amount of T cells with a stochastic description of the number of cancerous cells, I was able to investigate what happens to the eradication process when low numbers of pathogenic entities remained. By simulating the eradication process in this way, I was able to determine the probability that a disease would be eradicated given the number of eradicating agents and pathogens present at the start of the simulation.
- T cell antigen receptor membrane peptide: Structure, function and activity mechanism (Prof. Alison Rodger, Chemistry)
Using circular dichroism, I investigated the secondary structure of a peptide derived from the T-cell antigen receptor. Liposomes made from L-α-phosphatidylcholine and cholesterol were used as model versions of those found in eukaryotic organisms, and I then used circular and linear dichroism to investigate the interaction between the peptide and the liposomes. I also used dynamic light scattering as a means of determining the size distribution of the liposomes.
PhD - The macromolecular machine of dividing bacteria: Modelling the interactions in the divisome
Supervisors: Corinne Smith (Biological Sciences) and Matthew Turner (Physics)
Inhibiting the function of the Filamentous temperature sensitive (Fts) family of proteins causes the growth of long filamentous cell shapes. Since their inactivation is not directly lethal to the cell, each protein must play some role in cell division. Some of them have a known role in the divisome complex that orchestrates the division of a cell into two daughter cells.
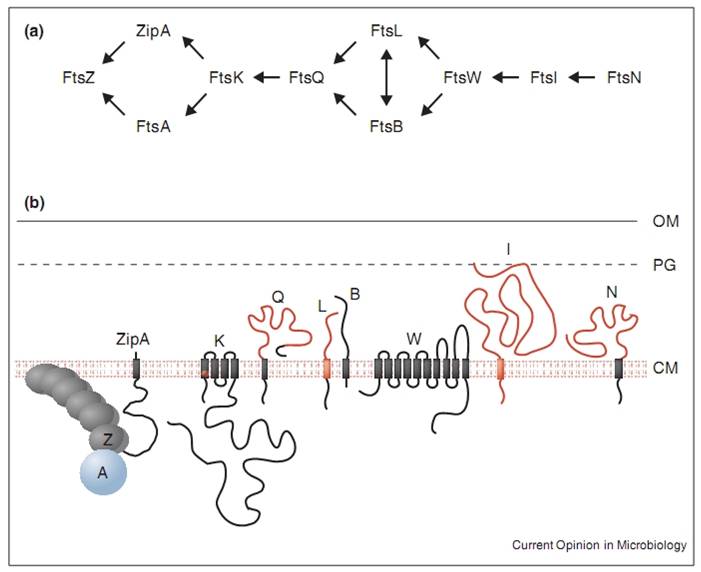
My research is centred around the protein FtsZ, which assembles into a ring at the future site of the septum of bacterial cell division, commonly known as the Z-ring. The polymerisation of FtsZ is facilitated by the binding of the protein to guanosine triphosphate (GTP), which forms FtsZ dimers. The Z-ring is then formed from protofilaments formed from a repeating arrangement of these dimers. GTP hydrolysis during assembly is probably balanced by rapid exchange of the GDP for the abundant GTP within the cell. The protofilaments are bundled together and anchored to the cytoplasmic membrane by several protein factors, such as ZipA and FtsA. An unknown signal triggers ring contraction and probable disassembly; this may involve stimulation of GTP hydrolysis, which would increase the number of GDP-bound subunits at protofilament ends, causing the formation of curved protofilaments.
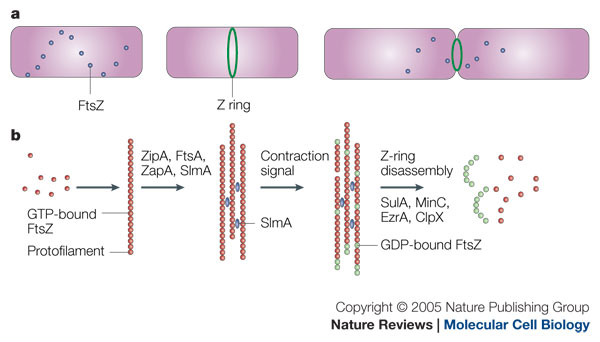 My work on this project to date has been in the following areas:
My work on this project to date has been in the following areas:
- Expression and purification of FtsZ
One of the first things I needed to do was create my own stock of FtsZ by expression in E. coli. Once the culture is grown, the cells are lysed and the extract taken from them is purified using ion exchange chromatography. The entire process takes one to two weeks to fully complete, but is not always successful. Once the purification is complete, activity of the FtsZ is checked by using a light scattering assay - if the FtsZ is active and polymerises upon the addition of GTP, then the presence of protofilaments should result in an increase in light scattering.
- Electron microscopy of FtsZ protofilaments
By using electron microscopy, it is possible to visualise the protofilaments which are formed by FtsZ polymerisation with GTP. Most of the time which I have spent on the electron microscopy has been experimenting with the polymerisation conditions (concentrations of FtsZ and GTP, time between GTP addition and staining, etc.) in order to get images in which the filaments are not too crowded, but protofilaments are still formed. So far, I have only performed negative-stain EM while we experiment with the conditions for the images which suit our needs, but in the future I intend to use cryo-EM in order to intend clearer images and remove the possibility that the stain may be having an effect on the FtsZ filaments.
- Calculation of physical properties of FtsZ protofilaments
From the EM images, I am able to measure certain properties of the FtsZ filaments (length, curvature, midpoint deviation, etc.) after using an image processing program such as ImageJ. From this data, I can calculate estimates for the rigidity of an FtsZ protofilament, which essentially tells you how much force is required to bend a structure to a certain degree of curvature, and also their persistence length, which is a measure of the length of fibre required before it starts to be significantly bent due to thermal fluctuations. I hope that this information will be useful in future work, where I would like to look at the forces experienced by FtsZ filaments during contraction of the Z-ring.
![[Photo of Daniel Turner]](../daniel_turner.jpg)
Daniel Turner
daniel.j.turner@warwick.ac.uk
MOAC
Coventry House
University of Warwick
Coventry
CV4 7AL
