Simulating MHD oscillations
Direct observations of oscillations in flares are often difficult. For this reason, a common technique used to study these events remotely is numerical simulation. Codes such as LareXd (Arber et al. 2001) can solve the MHD equations in normalised form, and thus be used to simulate all kinds of MHD processes. For example, the MHD sausage mode is a symmetric density perturbation about the axis of a coronal loop. We can model such a loop as a straight slab of plasma between two fixed boundaries. These boundaries represent the solar photosphere.
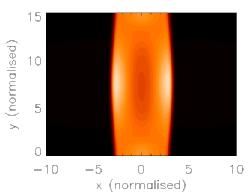
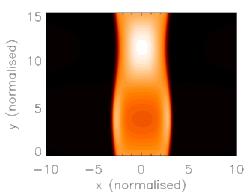
Image: Illustrations of the MHD sausage mode. The global mode (left) and the second harmonic (right) are both symmetric about the loop axis (x=0)
In many ways these waves can be thought of in the same way as you would consider standing waves on a string. There are some important differences however. For the sausage mode, there exists a critical length beyond which a standing wave cannot be supported. When the loop is much longer than this length, any excited wave quickly disappates into the surroundings. Although the existence of this cut-off can be mathematically shown and simulated, no obvious physical reason for it is apparent.
